Sort 알아보기(4) - 힙 정렬(Heap Sort)

Heap Sort

힙 정렬을 알기전에 우선 먼저 힙에 대해서 간략하게 보고 넘어가자면 힙은 완전 *이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이며 최댓값, 최솟값을 쉽게 추출할 수 있는 자료구조라고 한다. 힙에 대한 조금 더 자세한 내용은 다음 포스팅에서 힙을 구현해보며 설명 하려고 한다.

*이진 트리 : 모든 노드의 자식 노드가 2개 이하인 트리 구조

 

힙 정렬은 최대 힙 트리나 최소 힘 트리를 구성해 정렬하는 방법으로써 내림차순 정렬을 위해서는 최대 힙, 오름차순 정렬을 위해서는 최소 힙을 구성하면 된다.

과정을 내림차순을 기준으로 간략하게 정리해보자면

1. 정렬해야 될 n개의 데이터들로 최대 힙(완전 이진 트리 형태)를 만든다.

2. 한 번에 하나씩 요소를 힙에서 꺼내서 배열의 뒤에서 부터 저장하면 된다.

3. 삭제되는 데이터(이 경우 최댓값부터 삭제)는 값이 감소되는 순서로 정렬된다.

 

힙 정렬은 글로만 보면 이해가 잘 안갈 수도 있다. 그림으로 예시를 들어보자면

[10, 9, 5, 8, 3, 2, 4, 6, 7, 1] 이라는 배열을 오름차순으로 힙 정렬을 해보면

1. 데이터를 삽입한 배열을 완전 이진트리로 나타낸 다음 최대 힙의 루트 노드를 마지막 배열 값과 교환, 가장 큰 값을 마지막 배열에 저장하고 가장 크고 마지막 배열에 있는 데이터를 제거해준다.

2. 다시 힙을 재구조화 시키고 10을 제외한 최대 힙이 root자리로 다시 가게 된다.

3. 새로 생긴 최대 힙을 10을 제외한 마지막 데이터와 교환, 즉 root 노드인 9가 1이 있는 위치로 바뀌게 되고 9를 배열의 10을 제외한 가장 마지막에 저장하고 데이터를 제거해준다.

4. 이런 과정들을 반복해준다.

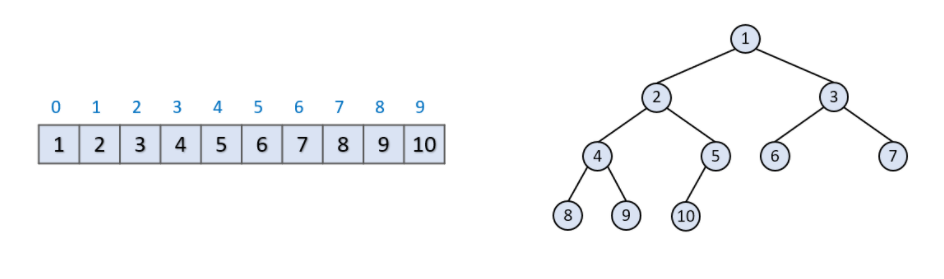
그러면 위와 같이 오름차순 정렬이 끝나게 된다.

 

특징

- 시간복잡도 부분에서 유리하다.

- 힙 정렬이 가장 유용한 경우는 전체 자료를 정렬하는 것이 아닌 가장 큰 값 몇개만 필요할 때 이다.

 

시간복잡도

- 힙 트리의 전체 높이가 거의 log₂n(완전 이진 트리이므로)이기 때문에 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재정비하는 시간이 log₂n만큼 소요된다.

- 요소의 갯수가 n개이므로 전체적으로 보면 T(n) = O(nlog₂n)의 시간이 걸린다.

정렬 시간복잡도 비교

참고 사이트

- https://gmlwjd9405.github.io/2018/05/10/algorithm-heap-sort.html

- https://underdog11.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Heapsort-%ED%9E%99%EC%A0%95%EB%A0%AC